Mathematica를 이용한 Fourier 급수 구하기

Fourier 급수를 간단히 설명하면 "모든 주기적인 (나중에 밝혀지지만 주기함수가 아니어도 됨)  함수는 sine 과 cosine의 합으로 구할 수 있다"는 것이다. 일반적으로 Fourier 급수는 상수, sine 함수, cosine 함수의 합으로 주어지며, 각각의 sine과 cosine 항에는 각기 다른 계수 (coefficient)가 붙는다.

 

그 예로서, 다음의 톱니함수의 푸리에 급수를 구해보자.

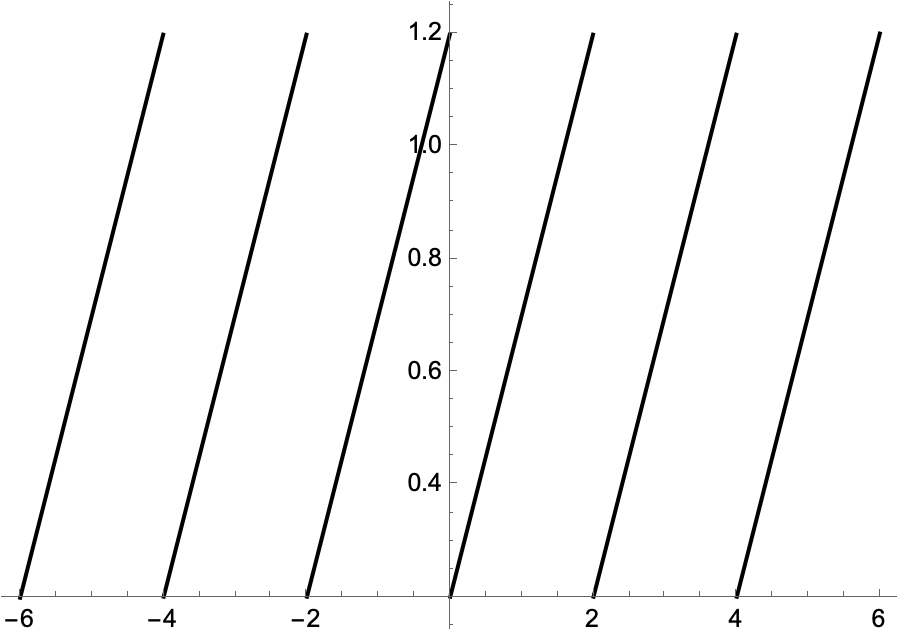
방법 1)

 

이 함수는 매스매티카에서 SawtoothWave[t/2] + 0.2 로 함수를 표현할 수 있다.  5번째 항까지의 푸리에 급수는 다음과 같이 구할 수 있다. 이 함수를 그래프로 그리려면 다음과 같이 실행하면 된다.

Plot[SawtoothWave[t/2]+0.2,{t,-6,6}]

그리고, 푸리에 급수는 매스매티카의 내장 명령인 FourierSeries 을 이용해 다음과 같이 구할 수 있다. 아래의 예는 5번째항 까지를 구하라는 명령어이다.

FourierSeries[SawtoothWave[t/2] + 0.2, t, 5,  FourierParameters -> {0, Pi}]

 

결과는 다음과 같다.

이 결과를 그래프로 그려보면, 다음과 같다.

 

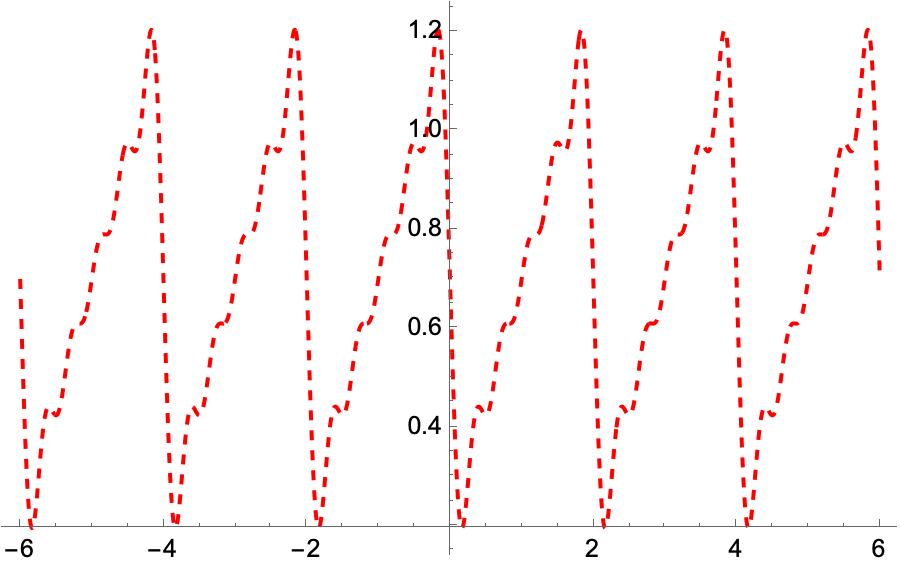
 두 함수를 함께 그려보면, 다음과 같은 결과를 얻을 수 있다.

 

Fourier 급수의 5번째 항까지 고려한 함수의 그래프와 톱니파와의 비교

푸리에 급수의 5번째 항으로 근사한 함수가 원래의 톱니파와 잘 일치함을 알 수 있다. 만약 더 많은 급수항을 추가하면, 원래의 함수에 근접하게 된다.  아래의 그래프는 20번째항과 100번째 항까지 추가한 함수의 그래프이다. 

Fourier 급수의 20번째 항까지 고려한 함수의 그래프와 톱니파와의 비교

Fourier 급수의 100번째 항까지 고려한 함수의 그래프와 톱니파와의 비교

항의 갯수가 증가하면, 처음의 톱니파 형태로 근접함을 알 수 있다.

 

방법 2)

 

그림의 톱니파는 -2에서 2 구간에서 주기함수로 정의되었므로, 다음과 같이 함수를 표현할 수 있다.

푸리에 급수의 상수항과 사인항 , 코사인항은 다음과 같이 주어진다.

따라서,  이를 매스매티카로 프로그래밍하면 다음과 같다. T=2 이므로(주기가 바뀔수 있으므로 T=2로 초기로 정해도 된다.

 

y1[t_]:=1/2 t + 1.2 ;

y2[t_]:=1/2t + 0.2;

T=2;

a0= (Intergrate[y1[t],{t,-2,0}] + Integrate[y2[t],{t,0,2}] )/ (2*2)

a[n_]:=(Intergrate[y1[t]*Sin[(n*Pi*t)/T],{t,-T,0}] + Integrate[y2[t]*Sin[(n*Pi*t)/T],{t,0,T})/T;

b[n_]:=(Intergrate[y1[t]*Cos[(n*Pi*t)/T],{t,-T,0}] + Integrate[y2[t]*Cos[(n*Pi*t)/T],{t,0,T})/T;

y[t_]:= a0 + Sum[a[n] * Cos[(n*Pi*t)/T] + b[n]*Sin[(n*Pi*t)/T], {n,0,20} ] (*sum over 20th terms*)

Simplify[y[t], T > 0] (* to simply y[t] due to y[t] is complicated. *)
T = 2;
Plot[sol, {t, -6, 6}, PlotStyle -> Directive[Red, Dashed] ]

 

이 코드를 실행하면 다음과 같은 결과를 얻을 수 있다. 처음의 톱니파와 비교하면 매우 근사함을 알 수 있으며, 방법 1로 구한것과 결과가 같음을 알 수 있다.

 

푸리에 급수의 20번째 항까지 고려한 함수의 그래프

 

푸리에 급수의 20번째항 까지 고려한 그래프와 톱니파와의 비교